Механика

ВИРТУАЛЬНАЯ ЛАБОРАТОРНАЯ РАБОТА № 4

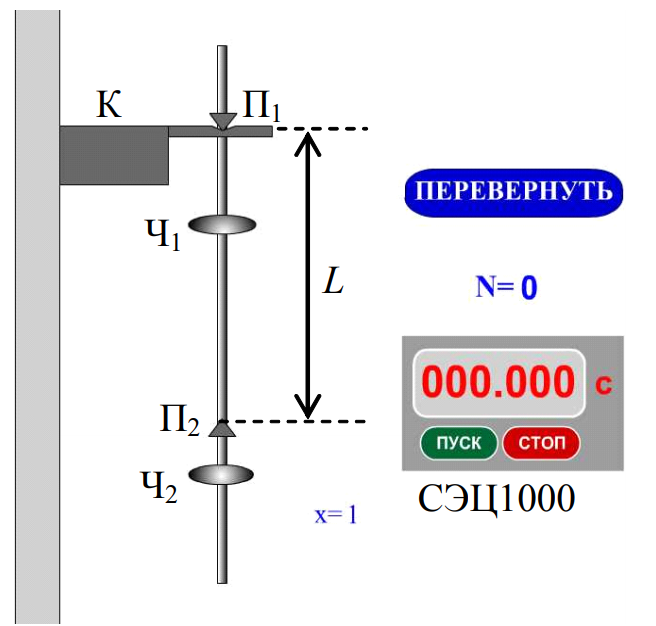
Определение ускорения свободного падения с помощью оборотного маятника (метод Бесселя) Цель работы: Исследовать закономерности колебаний физического маятника, экспериментально определить ускорение свободного падения. Приборы и принадлежности: виртуальный оборотный маятник; виртуальный электронный секундомер.

Описание виртуальной установки

Установка представлена на рис.1. Оборотный маятник представляет собой особый физический маятник для измерения ускорения свободного падения. Существуют различные конструкции оборотных маятников, но все они имеют две параллельные оси подвеса. Если период колебаний относительно обеих осей совпадает, расстояние между осями является приведенной длиной такого физического маятника. В некоторых маятниках для достижения совпадения периодов колебаний изменяют расстояние между осями подвеса маятника. В других расстояние между осями оставляют постоянным, а совпадения периодов добиваются перераспределением масс тел, входящих в состав маятника. Оборотный маятник в нашей установке относится ко второму типу. Он состоит из стержня (С), двух массивных чечевиц (Ч1 и Ч2) и двух треугольных призм (П1 и П2), остро заточенные грани которых являются осями подвеса маятника. При подвешивании маятника острая грань призмы для устойчивости размещаются в небольшом углублении закрепленного на стене кронштейна (К). В процессе измерения положение чечевицы Ч2 может меняться. Ее перемещением можно добиться того, чтобы периоды колебаний маятника Т1 и Т2 относительно обеих призм совпадали. В нашей виртуальной установке чечевицы Ч2 может фиксироваться в шести различных положениях (x = 1, 2,…6). Положение чечевицы отображается в текстовом поле справа от нее. Перемещение чечевицы о выбранного положения осуществляется «перетаскиванием» с помощью мыши при нажатой левой кнопке. При отпускании кнопки мыши чечевица фиксируется в ближайшем к курсору дискретном положении. Перемещение подвижной чечевицы возможно только, когда она находится в нижнем положении (маятник подвешен за призму П1). Переворачивание маятника (подвешивание за другую призму) осуществляется нажатием кнопки «ПЕРЕВЕРНУТЬ». При этом положение подвижной чечевицы сохраняется. Измерение времени осуществляется виртуальным электронным секундомером (СЭЦ1000). При нажатии кнопки «ПУСК» секундомера (левой кнопкой мыши) происходит его «обнуление». Если затем кнопку тпустить, то секундомер запустится, а маятник получит начальный «толчок» и начнет совершать колебания. Число полных колебаний, совершенных маятником, отображается в текстовом поле над секундомером. Важным достоинством установки является автоматическое отслеживание фазы колебаний. Это означает, что если кнопка «СТОП» нажата в любой момент времени, пока в текстовом поле отображается номер N конкретного колебания, после остановки на секундомере отобразится время, соответствующее точной фазе завершения N-ого полного колебания. В реальной установке включение и выключение секундомера в нужной фазе срабатывает при прохождении небольшого укрепленного на стержне магнита мимо неподвижно закрепленного геркона. Параметры виртуальной установки: L = 0,90 м – расстояние между призмами. Методика выполнения работы Добиться полного совпадения периодов колебаний путем непрерывного перемещения чечевицы достаточно трудно. Поэтому в работе используется следующий метод. Измеряют периоды колебаний Т1 и Т2 относительно обеих призм при различных фиксированных положениях чечевицы Ч2. Затем строят график зависимости периодов от положения чечевицы. В точке пересечения графиков периоды колебаний равны: Т1 = Т2 = Тоб. В этом случае расстояние между призмами равно приведенной длине физического маятника L. 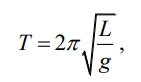Как известно, период колебаний физического мятника определяется выражением где L – приведенная длина маятника, а g – ускорение свободного падения. Откуда: 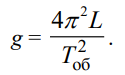(1) Формула (1) является основной расчетной формулой нашей работы. Оценка систематической погрешности Для оценки систематической погрешности используем процедуру, описанную в работе 1. 1. Прологарифмируем выражение (1) 2. 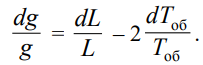Найдем полный дифференциал 3. Заменим минус на плюс, а дифференциалы на погрешности измерений: 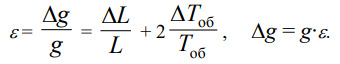При вычислении относительной погрешности ε можно считать, что погрешность измерения расстояния ΔL =1 мм. Погрешность измерения периода зависит от числа колебаний, учитываемых при определении периода: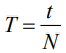. Поэтому, если погрешность измерения времени равна Δt, то погрешность измерения периода будет в N раз меньше. Однако, погрешность определения периода оборотного маятника нашим методом зависит, в основном, от качества построения графика. Для определенности будем считать ΔТоб = 0,01 с Обработка экспериментальных результатов. 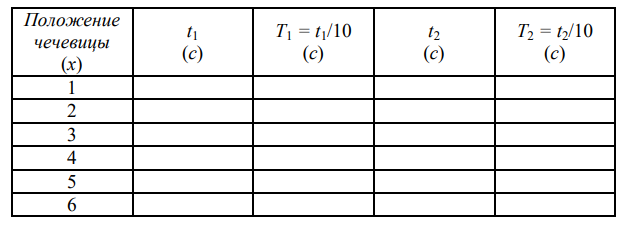1. Заготовьте таблицу (таблица 1)*. 2. Для заполнения таблицы запустите ролик с флэш-анимацией (виртуальная установка Pendulum.swf или Pendulum.exe). 3. Подвесьте маятник за призму П1 (по умолчанию при загрузке) и установите чечевицу Ч2 в выбранное положение (по умолчанию при загрузке x = 1). Запишите значение в x таблицу. 4. Измерьте время 10 полных колебаний маятника, для чего «кликните» кнопку «ПУСК» секундомера и следите за текстовым полем, отображающим число колебаний. Когда N станет равным 10, нажмите кнопку «СТОП». Запишите отображаемое секундомером время t1 в таблицу. 5. Переверните маятник (кнопкой «ПЕРЕВЕРНУТЬ»), подвесив его за призму П2, и повторите пункт 4. Запишите в таблицу время t2. 6. Повторите пункты 3-5 для шести положений чечевицы Ч2. Запишите полученные данные в таблицу. 7. Вычислите значения периодов Т1 и Т2. Занесите их в таблицу. 8. Постройте на одном графике зависимости Т1(x) и Т2(x) **. Для достижения большей точности можно выбрать следующий масштаб: ось x (1÷6), ось y (1,8÷2,1) с. 9. Определите по графику значение Тоб (точка пересечения кривых). 10.Рассчитайте g и Δg по формулам (1) и (2). 11.Сделайте вывод по работе.

*Таблицу с вычислениями удобно заготовить в редакторе Excel, внеся в столбцы необходимые для расчета формулы. **График удобно строить в редакторе Excel, используя данные столбцов 1, 3 и 5.

Контрольные вопросы*

1. Запишите уравнение гармонического колебания. 2. Дайте определение частоты, циклической частоты, периода, амплитуды, элонгации, фазы гармонического колебания. 3. Найдите скорость точки при гармоническом колебании. Найдите ускорение колеблющейся точки. 4. Выведите дифференциальное уравнение гармонического колебания для физического, математического и пружинного маятников. 5. Какому условию удовлетворяет сила, действующая на материальную точку, совершающую гармоническое колебание? Какая сила называется квазиупругой? Чему равен период колебания точки массой m под действием квазиупругой силы? 6. Найдите выражение для кинетической и потенциальной энергии колеблющейся точки. Чему равна полная энергия? 7. Дайте определения математического и физического маятников. Чему равны периоды их колебаний? 8. Какой маятник называется оборотным? 9. Что такое приведенная длина физического маятника? 10. Для каких целей производится измерение времени десяти, а не одного колебания? * Для подготовки к ответу на контрольные вопросы используйте лекции и учебники