Автор статьи
Валерия
Эксперт по сдаче вступительных испытаний в ВУЗах
Практическое задание по теме: «Моделирование»
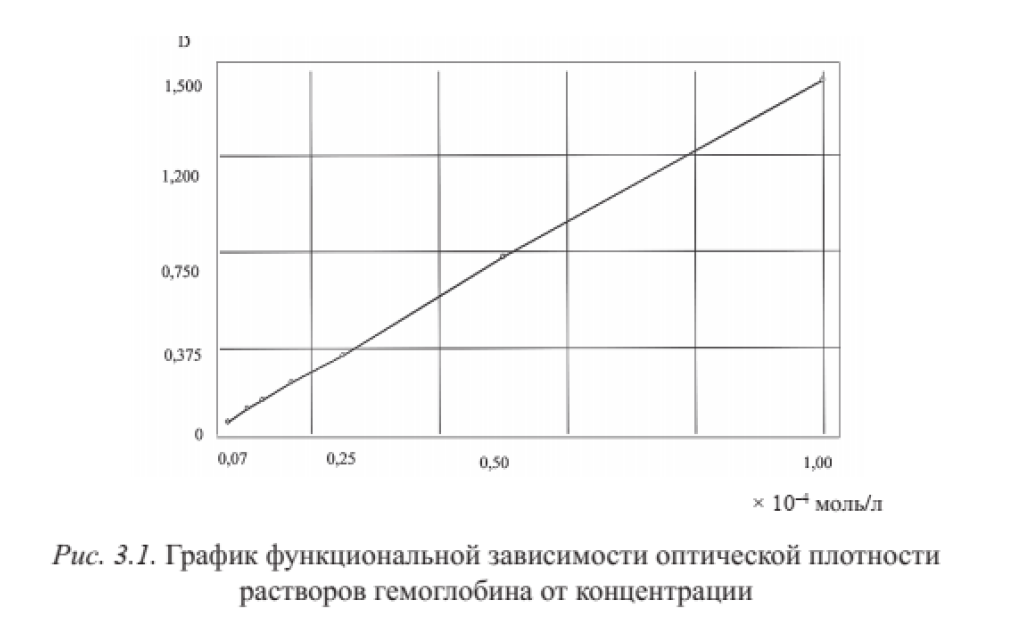
Часто при выполнении лабораторных работ, проведении экспериментальных исследований мы сталкиваемся с необходимостью определения концентрации вещества, его молекулярной массы и т. д. по показателям, зарегистрированным с помощью приборов. Решение такого рода задачи сводится к определению характера зависимости между регистрируемой и неизвестной переменными и последующей подстановке в уравнение измеренного значения для вычисления искомой величины. Оптимальным является вариант, когда зависимость носит линейный характер или ее можно линеаризовать с помощью несложных преобразований исходных показателей (например, путем двойного обратного преобразования системы координат, логарифмирования и т. д.). Рассмотрим в качестве примера метод определения концентрации гемоглобина в растворе по величине его оптической плотности. Известно, что эти величины связаны между собой линейной зависимостью в довольно широком диапазоне концентраций. Для получения данных для построения модели нужно приготовить раствор исследуемого вещества в известной концентрации (10–4 Моль/л). Измерить оптическую плотность опытного раствора при заданной длине волны (например, 576 нм). Разбавить исходный раствор в 2, 4, 6, 8, 10 и 15 раз. Измерить оптическую плотность раствора с неизвестной концентрацией. Данные занести в таблицу (табл. 3.1). По зарегистрированным данным можно построить график зависимости оптической плотности раствора гемоглобина от его концентрации и по нему определить искомую величину. Однако определение положения точки на прямой (или кривой) всегда сопряжено с определенной ошибкой. Более точную информацию можно получить, разработав простую математическую модель, т. е. 92 подобрав уравнение, которое описывало бы данную зависимость. Тогда, подставляя в полученное уравнение измеренные значения х, можно будет точно вычислить искомое значение у.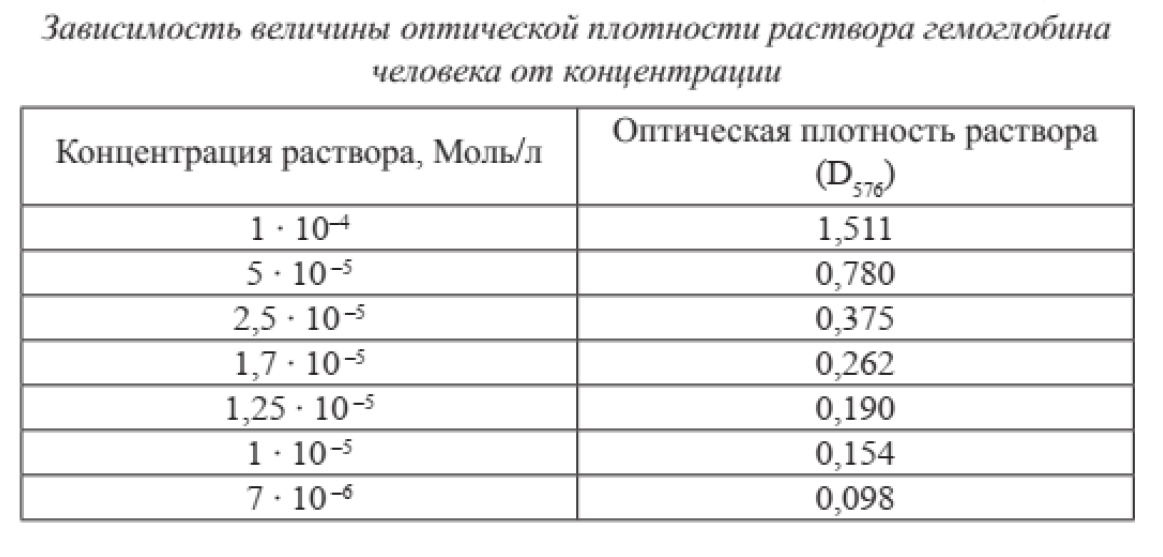
Перед выбором модели для получения представления о характере зависимости y от x целесообразно построить функциональный график и провести его визуальный анализ (рис. 3.1).
Легко заметить, что график имеет линейную форму, отражающую прямо пропорциональную зависимость между исследуемыми показателями.
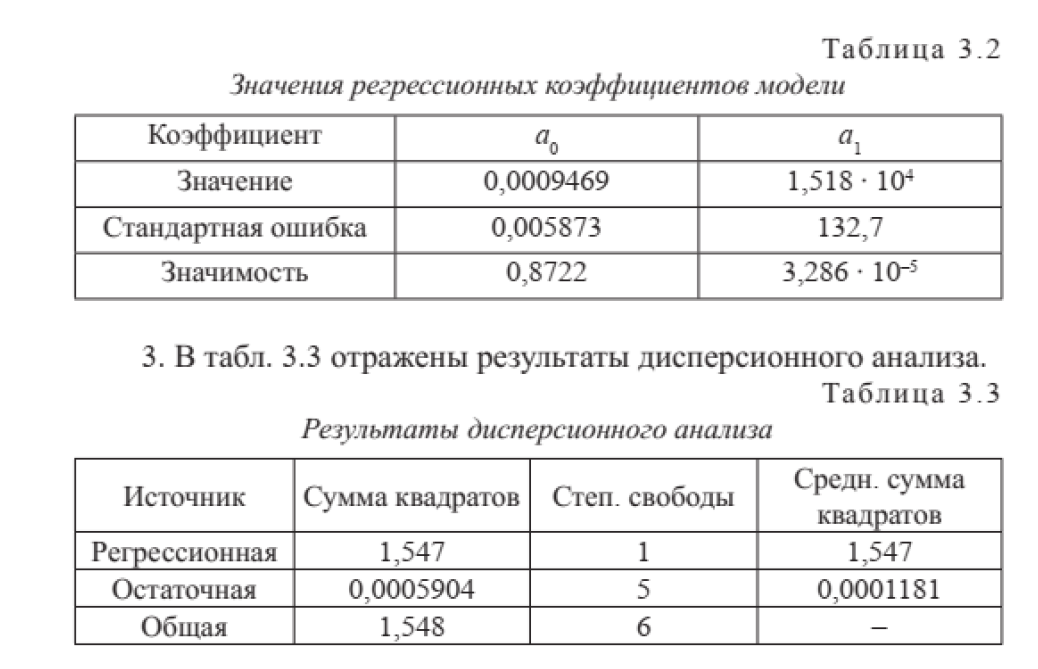
Для построения математической модели воспользуемся возможностями пакета прикладных статистических программ STADIA. В разделе «Регрессионный анализ» выберем пункт «Простая регрессия». Зададим зависимую (у) и независимую (х) переменные из электронной таблицы для анализа. Данный этап анализа очень важен, так как зависимости y = f(x) и x = f(y) не идентичны. Поэтому к выбору зависимой и независимой переменных следует отнестись предельно внимательно. Результаты анализа: 1. Уравнение регрессии, или модель, записанная в общем виде: у = a0 +a1 · x. 2. В табл. 3.2 приведены значения коэффициентов модели со стандартными ошибками вычисления каждого коэффициента.
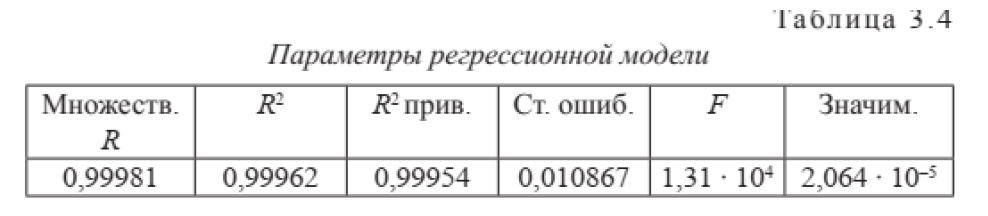
4. В табл. 3.4 приведены следующие параметры: множественный коэффициент корреляции R; R2 (квадрат R или коэффициент детерминации); приведенная, или несмещенная, оценка R2 ; значение критерия Фишера (F) и уровень значимости Р нулевой гипо- 94 тезы о равенстве нулю коэффициента множественной корреляции. Принятие этой гипотезы означает отсутствие корреляции между исходными данными и математической моделью, иными словами – модель неадекватно описывает экспериментальные данные. Если Р > 0,05, нулевая гипотеза может быть принята.
Затем можно построить регрессионный график, на котором изображаются экспериментальные данные с регрессионной кривой и зона стандартной ошибки регрессии. На регрессионном графике (рис. 3.2) экспериментальные точки не выходят за пределы доверительного интервала. Следовательно, графиком можно пользоваться как калибровочной прямой для определения концентрации вещества в растворе.
5. Вывод. Как следует из числовых результатов, линейная модель адекватна экспериментальным данным по F-критерию Фи- шера (значимость нулевой гипотезы близка к нулю). Часть коэффициентов уравнения статистически не значима, поэтому модель пригодна для принятия решений, но не для прогнозов. Поскольку регрессию вообще не следует экстраполировать за пределы проведенных опытов, так как она может поменять свое направление, предлагаемая модель полностью отвечает поставленной задаче (определение концентрации вещества по величине его оптической плотности). Таким образом, записав уравнение у = a0 +a1 · x в окончательном виде: у = 0,0009469 + 1,518 · 104 · x и подставляя вместо х измеренные значения оптической плотности, можно рассчитать концентрацию гемоглобина в растворе.
О сайте
Ссылка на первоисточник:
http://www.mesi.ru
Поделитесь в соцсетях: