Практическая работа по дисциплине «Биология» для ВГУ, пример оформления

Практическое задание «Работа с собственными экспериментальными данными»

Рассмотрим пример анализа данных по приведенному выше алгоритму.

1. Постановка задачи исследования и планирование эксперимента.

Цель исследования состояла в изучении электрофоретических характеристик нитрозогемоглобина (HbNO) человека. Одной из задач являлось определение содержания белка во фракциях HbNO.

2. Сбор первичных данных осуществлялся в ходе обработки результатов экспериментов. Были построены денситограммы образцов HbNO (рис. 2.2), и по площади пика, соответствующего данной электрофоретической фракции, рассчитано относительное содержание белка в ней.

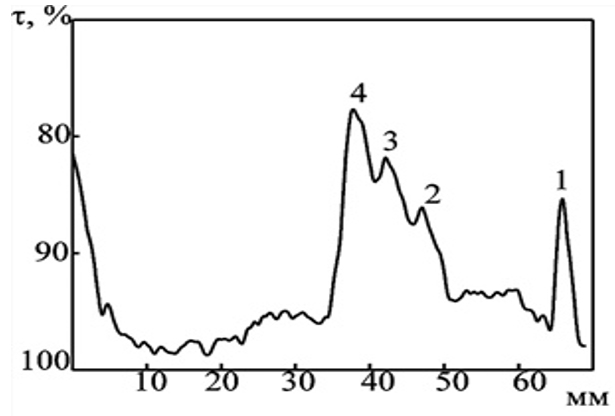
Рис. 2.2. Денситограмма нитрозогемоглобина человека. Обозначения: по оси ординат: τ – светопоглощение геля, %; по оси абсцисс: длина геля, мм.

3. Систематизация результатов исследования, ввод и сохранение данных в электронном архиве.

Систематизация результатов по расчету содержания белка во фракции данных представляет в этом случае составление простой таблицы (табл. 2.3) и перенос значений показателей в электронную таблицу

4. Визуальное изучение данных в графическом виде.

Анализируемые данные не представляют собой функциональной (или какой-либо иной) зависимости, объем их невелик, поэтому построение графиков нецелесообразно.

5. Редактирование и выполнение различных преобразований данных.

Проверим соответствие данных в электронной таблице данным в лабораторном журнале (нет ли опечаток и пропусков). Никакого дополнительного редактирования (ранжирования, замены качественных данных цифровыми символами и т. д.) и преобразований не требуется.

6. Выбор и исполнение соответствующего метода анализа.

Все процедуры статистической обработки были проведены нами с помощью пакета прикладных статистических программ «STADIA», поэтому в приводимых примерах мы будем использовать тот формат представления данных и результатов, который предлагает данная программа. Для наглядного представления о типе распределения исследуемой характеристики полезно построить вариационный ряд и гистограмму распределения. Гистограмма является общеупотребительной формой представления выборочного распределения. Для ее вычисления диапазон изменения выборочных значений разбивают на некоторое число равных интервалов (бинов) и подсчитывают число значений, попадающих в каждый бин. При графическом представлении гистограммы на каждом интервале строится столбец, высота которого пропорциональна числу выборочных значений в данном интервале. Для каждого интервала гистограммы рассчитываются следующие значения: левая граница интервала в исходных единицах (Хлев.) и единицах стандартного отклонения (Х станд.); частота класса, или интервала, – число выборочных значений, попавших в данный интервал, выраженное в абсолютных (Частота) и относительных (%) единицах; сумма накопленных частот – накопленное число выборочных значений до текущего интервала включительно в абсолютных (Накопл.) и относительных (%) единицах (табл. 2.4). Проверка выборочного распределения на нормальность проводится с целью верификации нулевой гипотезы об отсутствии различий между выборочным и нормальным распределениями по трем критериям (Колмогорова, омега-квадрат (ω2) и хи-квадрат (χ2) Пирсона) с уровнем значимости Р:

• Колмогоров=0,1722, Значимость=0,5258, степ.своб = 10.
• Гипотеза 0: Распределение не отличается от нормального.
• Омега-квадрат=0,03375, Значимость=0,5857, степ.своб = 10.
• Гипотеза 0: Распределение не отличается от нормального.
• Хи-квадрат=0,5115, Значимость=0,4745, степ.своб = 1.
• Гипотеза 0: Распределение не отличается от нормального.

Для полного описания варьирующих объектов служат особые, логически и теоретически обоснованные числовые показатели, называемые статистическими характеристиками. К ним относятся, прежде всего, средние величины и показатели вариации. В отличие от индивидуальных числовых характеристик средние величины обладают большей устойчивостью, способностью характеризовать целую группу однородных единиц одним (средним) числом. Значение средних заключается в их свойстве аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее среднее и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяет отличать один объект от другого. Сначала вычисляются основные выборочные характеристики: размер выборки, диапазон значений, выборочное среднее, ошибка среднего, выборочные дисперсия и стандартное отклонение (табл. 2.5). Содержание белка во фракции, % характеризовать целую группу однородных единиц одним (средним) числом. Значение средних заключается в их свойстве аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее среднее и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяет отличать один объект от другого. Сначала вычисляются основные выборочные характеристики: размер выборки, диапазон значений, выборочное среднее, ошибка среднего, выборочные дисперсия и стандартное отклонение (табл. 2.5). Далее по подтверждению может быть выдана дополнительная статистика: медиана, квартили, размах доверительного интервала среднего, границы доверительного интервала дисперсии, ошибка стандартного отклонения (табл. 2.6).

7. Представление полученных результатов в числовой, табличной и графической формах.

Поскольку объем анализируемых данных и полученных результатов невелик, то оптимальным вариантом представления данных будет их простое словесное описание (см. выводы). Данные о перераспределении белка между фракциями при воздействии на образцы белка, например УФ-излучения, наиболее выгодно было бы представить в виде накопленной диаграммы (см. рис. 2.1).

8. Выводы по результатам анализа.

Наблюдается тенденция к накоплению частот в средних классах выборки. Согласно результирующим уровням значимости всех трех критериев (Р > 0,05), можно признать гипотезу о нормальном распределении содержания белка в данной электрофоретической фракции нитрозогемоглобина человека. Выборка характеризуется средним значением содержания белка во фракции 17,92 % при стандартном отклонении 3,86 %. Следует отметить, что среднее (17,92 %) и медиана (17,65 %) имеют близкие по величине абсолютные значения, межквартильные интервалы симметричны относительно центрального значения (11,00 – 15,45; 15,45 – 17,65; 17,65 – 20,43; 20,43 – 24,70). Это является дополнительным подтверждением нормальности распределения исследуемого признака и подтверждает правомерность использования среднего арифметического и стандартного отклонения в качестве характеристик исследуемой выборки.