Решение задач по специальности «Методы принятия управленческих решений»

Дисциплина: Методы принятия управленческих решений. Задание 1 1 Постановка транспортной задачи как задачи линейного программирования. Закрытая и открытая модель транспортной задачи. Приведите примеры. Транспортная задача (ТЗ) является важнейшей частной задачей линейного программирования, имеющей обширные практические приложения не только к проблемам транспорта. Она выделяется в линейном программировании определённостью экономической характеристики, особенностями математической модели, наличием специфических методов решения. Наиболее часто встречаются следующие задачи, относящиеся к транспортным: — прикрепление потребителей ресурса к производителям; — привязка пунктов отправления к пунктам назначения; — взаимная привязка грузопотоков прямого и обратного направлений; — отдельные задачи оптимальной загрузки промышленного оборудования; — оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др. Модель ТЗ называют закрытой (сбалансированной), если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т. е. выполняется равенство:

2 Чему равен ранг системы нетривиальных ограничений транспортной задачи? Дайте определение опорного решения и приведите пример его построения.

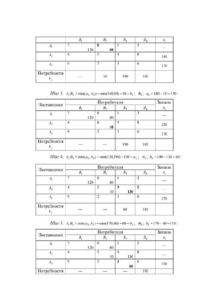
Ранг матрицы системы ограничений транспортной задачи равен r(A)  ъp 1 m  n 1. Опорным решением транспортной задачи называется любое допустимое решение, для которого столбцы матрицы системы ограничений, соответствующие положительным значениям линейно независимы. Пример: Рассмотрим три основных метода построение начального опорного плана транспортной задачи: 1 метод северо-западного угла, 2 метод минимального тарифа. Сущность этих методов состоит в том, что начальный опорный план находят за m+n-1 последовательных шагов, на каждом из которых в транспортной таблице заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка). В первом случае временно исключают из рассмотрения столбец, содержащий заполненную на данном шаге клетку, и рассматривают задачу, таблица которой содержит на один столбец меньше, чем было перед этим шагом, но то же количество строк и соответственно измененные запасы груза в одном из пунктов отправления (в том, за счет запаса которого была удовлетворена потребность в грузе пункта назначения на данном шаге). Во втором случае временно исключают из рассмотрения строку, содержащую заполненную клетку, и считают, что таблица условий имеет на одну строку меньше при неизменном количестве столбцов и при соответствующем изменении потребности в грузе в пункте назначения, в столбце которого находится заполняемая клетка. После того как проделаны m + n — 2 описанных выше шагов, получают задачу с одним пунктом отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают (m + n -1)-й шаг и получают искомый опорный план. Следует заметить, что на некотором шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправления. В этом случае также временно исключают ив рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение m + n — 1 занятых клеток, в которых стоят компоненты опорного плана, что является исходным условием для проверки последнего на оптимальность и нахождения оптимального плана. Метод северо-западного угла При нахождении опорного плана транспортной задачи методом северо- западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы начинается с левой верхней клетки для неизвестного х11 («северо-западный угол») и заканчивается клеткой для неизвестного хmn, то есть идет как бы по диагонали таблицы из левого верхнего угла в правый нижний угол.

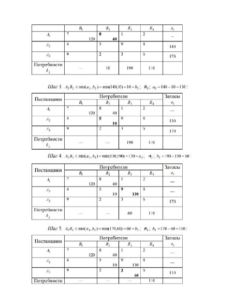
Метод минимального тарифа

При использовании метода северо-западного угла на каждом шаге потребности первого из оставшихся пунктов назначения удовлетворялись за счет запасов первого из оставшихся пунктов отправления. Выбор пунктов назначения и отправления целесообразно производить, ориентируясь на тарифы перевозок, а именно: на каждом шаге следует выбирать какую- нибудь клетку, отвечающую минимальному тарифу (если таких клеток несколько, то следует выбрать любую из них), и рассмотреть пункты назначения и отправления, соответствующие выбранной клетке. В этом и состоит сущность метода минимального тарифа. Этот метод, как правило, позволяет найти начальное опорное решение транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла. Пример метода минимального тарифа для транспортной таблицы из примера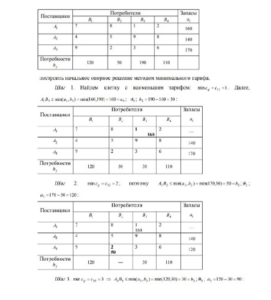

6 Сформулируйте определения следующих понятий: свободная клетка, занятая клетка, оценка свободной клетки, цикл, перестановка по циклу. В чем состоит условие оптимальности опорного плана?

Клетки таблицы транспортной задачи, в которых находятся отличные от нуля или базисные нулевые перевозки, называются занятыми, остальные – незанятыми или свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку х ij , т.е. стоящая в i -й строке и j -м столбце, имеет номер i, j. Каждой клетке с номером i, j соответствует переменная ij x , которой соответствует вектор-условие Aij (соответствующий столбец матрицы ограничений). Для проверки линейной независимости векторов-условий, соответствующих положительным элементам ij x допустимого решения, вводят понятие цикла. Циклы также используются для перехода от одного опорного решения к другому.

Задание 2

1 Общая постановка задач многокритериальной оптимизации. Примеры задач с экономическим содержанием. Многокритериальная задача оптимизации – математическая модель принятия оптимального решения одновременно по нескольким критериям. Эти критерии могут отражать оценки различных качеств объекта (или процесса), по поводу которого принимаются решения. Наиболее распространенная задача, когда требуется найти решение, для которого достигались наилучшие значения сразу по нескольким критериям — это поиск покупки, которая была как можно качественнее и как можно дешевле. Многокритериальные задачи, которые не просто решить исходя только из интуитивных соображений, возникают в разнообразных видах человеческой деятельности. Например, при проектировании компьютера может быть поставлена задача, в рамках которой формируется конфигурация, при которой одновременно достигаются максимальное быстродействие, наибольшая оперативная память и наименьший вес компьютера. Пример задачи: Определить тип задачи и найти оптимальное решение, всеми способами. Фирма имеет возможность реализовывать свои товары на 4-х различных рынках (альтернативы A1 A2, А3 А4). При этом ставятся одновременно следующие цели: минимизация затрат на рекламу, завоевание максимальной доли рынка и максимальный объем продаж в течение планируемого периода. Исходные данные приведены в таблице. В общем случае принцип доминирования по Парето является способом попарного сравнения всех альтернатив. Логически возможны следующие случаи: 1 по всем критериям альтернативы ai и aj эквивалентны, тогда альтернативы ai и aj эквивалентны с точки зрения принятия решений 2 по одним критериям альтернативы ai и aj эквивалентны, а по другим ai предпочтительнее альтернативы aj , тогда ai доминирует по Парето альтернативу aj 3 по одним критериям ai предпочтительнее альтернативы aj , а по другим – ai хуже альтернативы aj , тогда альтернативы ai и aj несопоставимы по Парето. В противном случае всегда найдется точка x, оказывающаяся более предпочтительной независимо от расстановки приоритетов и относительно важности отдельных частных критериев. Принцип Парето позволяет сузить класс возможных претендентов на окончательное решение и исключить из рассмотрения заведомо неконкурентноспособные варианты. А окончательный выбор осуществляется на основе дополнительной информации о предпочтении лица, принимающего решения. Введение понятия слабоэффективных решений вызвано тем, что в процессе оптимизации часто получаются решения, принадлежащие S(Д) (множеству слабоэффективных решений), но не принадлежащие P(Д) (множеству эффективных решений), а они, конечно, представляют меньший интерес по сравнению с эффективными решениями. 4 Дайте определение Парето-эффективной границы и приведите пример ее построения. Парето-оптимальность некоторого исхода означает, что он не может быть улучшен ни по одному из критериев без ухудшения по какому-либо другому критерию. Пусть совокупность функций осуществляет отображение множества допустимых решений на множестве . Подмножество называется эффективной границей (множество точек оптимальных по Парето), если для любого вектора не существует вектора , который доминирует вектор . Для наглядного представления доминирования по Парето и Парето- оптимальности рассмотрим случай двух позитивных критериев и . Критерий называется позитивным, если лицо, принимающее решение, стремиться к его увеличению, и негативным, если ЛПР стремится к его уменьшению. Векторные оценки исходов представим точками координатной плоскости. 5 Основные методы решения задач многокритериальной оптимизации.

Задание 3

1 Предмет теории игр. Примеры игровых моделей в экономике. Теория игр – это математическая дисциплина, разрабатывающая теоретические основы построения математических моделей принятия оптимальных решений в конфликтных ситуациях, носящих характер конкурентной борьбы, в том числе и в условиях неопределенности. Использование теории игр помогает лицу, принимающему решение, произвести критический анализ ситуации и в результате более обоснованно и последовательно проводить стратегию поведения при решении сложных проблем. Это означает, что с помощью теории игр можно: • смоделировать процесс и возможные результаты будущей игры еще до ее фактического начала; • по результатам моделирования будущей игры принять решение о целесообразности участия и оптимальном поведении в реальном конфликте. В настоящее время теоретико-игровые модели используются в различных областях экономики и других наук, в частности: • для выбора эффективных стратегий в бизнесе и оптимального поведения фирмы, • для рационального управления финансами, в теории инвестирования. Кроме того, теория игр используется : • в оценке эффективности проектов, • в страховании, • в управлении городским транспортом, • в области рынка жилья, • в теории инноваций, • в анализе и управлении эколого-экономическими системами,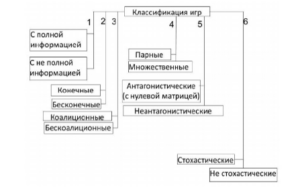 Игра, в которой множества А и В стратегий игроков конечны, т.е. |А| < ¥, |В|< ¥, называется матричной. В этом случае функция выигрышей игрока 1 имеет вид матрицы, называемой матрицей игры (матрицей выигрышей, платежной матрицей) Н = {аij}m,n, i = 1,…, т; j = 1,…, п. Строки этой матрицы соответствуют стратегиям a1, а2, …, аm игрока 1, столбцы — стратегиям b1, b2, …, bn игрока 2 Элемент матрицы aij = H (ai, bj) — выигрыш игрока 1 в случае, когда он применит стратегию аi, а его противник — стра- тегию bj, i = 1, …, т; j = 1, …, п. Элементы матрицы могут быть положительными, отрицательными или равными нулю. Случай, когда данный элемент матрицы положителен, означает, что игрок 2 в определенной ситуации должен уплатить игроку 1 сумму, равную значению этого элемента. Если данный элемент отрицателен, игрок 1 уплачивает игроку 2 сумму, равную абсолютному значению этого элемента. И наконец, если этот элемент равен нулю, никакой выплаты не производится. Таким образом, в игре двух лиц с нулевой суммой один игрок выигрывает столько же, сколько проигрывает другой (все выплаты производятся из «карманов» противников). Это и объясняет название — игра с нулевой суммой. Игрок 1 стремится к максимальному выигрышу, игрок 2 — к минимальному проигрышу. Решить игру — значит найти оптимальные стратегии игроков и их выигрыши. В игре двух лиц с нулевой суммой, как и в любой другой стра- тегической игре, исход зависит от поведения обоих игроков, которое основывается на так называемых правилах игры. Допустим, что по правилам игры игрок 1 может выбрать произвольную строку матрицы и, следовательно, может выбрать одно из чисел 1, 2, …, т. Аналогично игрок 2 имеет возможность выбора произвольного столбца матрицы выигрышей и, следовательно, одного из чисел 1, 2,…, п. Исход (результат) игры и, следовательно, сумму, которую игрок 2 должен уплатить игроку 1, определяет элемент матрицы выигрышей, находящийся на пересечении строки, выбранной игроком 1, и столбца, выбранного игроком 2 Ни один из партнеров не знает, какую стратегию применит его противник. Таким образом, имеет место ситуация полной неопределенности, при которой теория вероятностей не может помочь игрокам в выборе решения.

3 Оптимальные стратегии игроков. Верхняя и нижняя цена игры и соотношение между ними.

Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом ходе в зависимости от сложившейся ситуации. Стратегия может быть чистой – если игрок сознательно выбирает в качестве хода какое-либо из предусмотренных правилами действий. Стратегия может быть смешанной – если игрок комбинирует свои предусмотренные правилами действия. Для того чтобы найти решение игры, для каждого игрока необходимо выбрать такую стратегию, чтобы каждый из игроков должен был получить максимальный выигрыш в самой для себя неблагоприятной ситуации. Такие стратегии называются оптимальными.

4 Игра с седловой точкой. Решение игры в чистых стратегиях.

Приведите примеры игр с седловой точкой. Седловая точка – это ситуация равновесия (консенсус). Седловая точка является минимальным значением в k-й строке и максимальным в l-м столбце (основа для выработки алгоритма поиска консенсуса). Каждая седловая точка соответствует оптимальным стратегиям игроков. Кроме того, каждая седловая точка является одновременно и максиминной и минимаксной стратегией игроков. Таким образом, видно, что они совпадают. В игре без седловой точки ни у одного из игроков нет оптимальных чистых стратегий, несмотря на то, что у игрока А есть максиминные стратегии, а у игрока В – минимаксные. Алгоритмы поиска седловых точек: Алгоритм 1 1 Находим максиминное значение выигрыша игрока А. 2 Находим минимаксное значение проигрыша игрока В. 3 Если они равны, значит седловая точка есть. 4 Все пересечения максиминных и минимаксных стратегий игроков и являются седловыми точками. Алгоритм 2 1 Помечаем в каждой строке наименьшие элементы. 2 Отбрасываем те, которые не являются наибольшими в своих столбцах. 3 Оставшиеся элементы являются седловыми точками матрицы. В качестве примера решим следующую задачу. Финансовая компания В ведет переговоры с инициаторами трех инвестиционных проектов В1 В2 и B3/ Инвестиционный договор она может заключить только с одним из инициаторов проектов. Конкурирующая компания А ставит своей задачей свести переговоры компании В к отрицательному результату с тем, чтобы занять место компании В в инвестировании. Компания А для достижения своей цели может применить одно из двух средств: А1 — предложить инициаторам проектов более выгодные условия по сравнению с компанией В; А2 — предоставить материалы, компрометирующие компанию В. Действие A1 компании А приводит к отрицательному результату переговоров компании В с инициаторами проектов В1, В2 и В3 соответственно с вероятностями 0,7; 0,5; 0,3, а действие А2 — с вероятностями 0,6; 0,9; 0,4. Найти решение игры в чистых стратегиях. Распишем действия игроков. Игрок В должен выбрать один из трех проектов. Игрок А выбирает одно из двух своих действий. Игрок А имеет две чистые стратегии: А1 — предложить инициаторам проектов более выгодные условия по сравнению с компанией В; А2 — предоставить материалы, компрометирующие компанию В. Игрок В имеет три чистые стратегии: В1- выбрать первую компанию; В2- выбрать вторую компанию; В3- выбрать третью компанию; В этой игре выигрыш функции игроков не описываются аналитическим выражением. В качестве выигрыша игрока А (или проигрыша игрока В)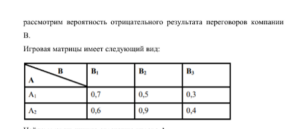 Комбинация игроком по какому-то своему правилу своих чистых стратегий называется смешанной стратегией. Основная теорема матричных игр Дж. фон Неймана: Любая матричная игра имеет решение в смешанных стратегиях, т.е. существуют цена игры в смешанных стратегиях V u оптимальные смешанные стратегии Р° u Q° соответственно игроков А и В, т.е. Поиск оптимальных смешанных стратегий имеет смысл, если в игре нет седловых точек.

6 Сведение матричной игры к задачам линейного программирования. Приведите примеры.

Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и решена симплексным методом и, наоборот, каждая задача линейного программирования может быть представлена как конечная игра двух лиц с нулевой суммой. Величина v неизвестна, однако можно считать, что цена игры v > 0 Последнее условие выполняется всегда, если все элементы платежной матрицы неотрицательны, а этого можно достигнуть, прибавив ко всем элементам матрицы некоторое положительное число. Преобразуем систему ограничений, разделив все члены неравенств на v. Аналогично для второго игрока оптимальная стратегия обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры. 1 В прямой задаче ищется максимум функции цели (линейной формы), а в двойственной задаче — минимум. 2 Коэффициенты при переменных в функции цели прямой задачи являются свободными членами системы ограничений двойственной задачи, и наоборот, свободные члены системы ограничений прямой задачи — коэффициентами при переменных в функции цели двойственной задачи. 3 В каждой задаче система ограничений задаётся в виде неравенств, причём все они одного смысла, а именно: при нахождении максимума функции цели (прямая задача) эти неравенства записываются со знаком «меньше или равно», а при нахождении минимума (двойственная задача) — со знаком «больше или равно».

4 Коэффициенты при переменных в системах ограничений описываются матрицами которые являются транспонированными относительно друг друга.

Задание 4 1 . Постановка задачи динамического программирования. Состояния системы. Управление. Уравнение состояний. Поясните смысл отсутствия последействия в динамической системе. Рассмотрим класс задач исследования операций, в которых процесс протекания операции является многошаговым, т.е. развернут во времени. Тат как этот класс задач описывает явно динамику процесса, то они получили название задач динамического программирования. В динамических задачах для описания состояний процесса удобно ввести еще одну группу переменных, называемых фазовыми переменными. Таким образом, при отсутствии неконтролируемых факторов в задаче динамического программирования у нас будет уже две группы переменных – фазовые переменные и стратегии, причем в соответствии с принятой в этом разделе исследования операций терминологией будем называть последние переменные управлением. Также в соответствии с принятыми обозначениями обозначим фазовые переменные буквами , а управляющие переменные – . Во избежание путаницы на этом стоит остановить внимание. В линейном и нелинейном программировании через обозначают переменные, по которым производится оптимизация целевой функции, т.е. которые выбирает оперирующая сторона. В динамическом программировании выбору подлежит управление, т.е. величины А переменные служат для описания процесса, т.е. для определения конечного результата (значения критерия эффективности) для тех или иных выбранных управлений. Будем рассматривать только многошаговые процессы, в которых время является дискретным и описывается номером шага, фазовые переменные и управление на -м шаге обозначаются. Число шагов предполагается конечным и равным Процесс протекания операции обычно описывается уравнением вида: Предположим, что исследуемая операция представляет собой процесс, развивающийся во времени и состоящий из серии этапов (или шагов). Существуют операции, которые распадаются на ряд шагов совершенно естественным образом (например, при разработке плана хозяйственной деятельности фирмы (предприятия) на долгосрочный период естественно принять год за один шаг). В других операциях такое деление можно выполнить искусственно, выбирая некоторую длину, интервал времени, в качестве продолжительности шага. Так как изучаемый процесс является управляемым, то на каждом шаге должно приниматься решение, от которого зависит успешное выполнение данного шага и операции в целом. Таким образом, управление всей операцией складывается из ряда элементарных, «пошаговых» управлений. Рассмотрим пример многошаговой операции планирования хозяйственной деятельности объединения (группы) промышленных предприятий Пi, П2, Пk на некоторый период времени Т, состоящий из m хозяйственных лет. Предположим, что в начале периода планирования на развитие группы предприятий выделены капитальные средства в размере К0, которые предназначены для расходования в процессе функционирования системы. Эти средства определенным образом должны быть распределены между предприятиями рассматриваемой группы. Считается, что предприятие за год приносит доход, величина которого зависит от вложенных средств. В начале каждого хозяйственного года сумма имеющихся средств должна быть перераспределена между предприятиями — каждому предприятию выделяется определенная доля средств. При разработке операции планирования возникает вопрос: как в начале года нужно распределять имеющиеся средства между предприятиями, чтобы суммарный доход от всей группы предприятий за весь период Т был максимальным? Предположим, что в начале некоторого года / предприятиям П1, П2, Пк выделяются соответственно средства Хi1, Хi2,… Xik. Совокупность этих значений представляет собой не что иное, как управление на шаге i: Ui=(Xi1, Хп,… , Х!к). А управление операцией в целом выражается как совокупность всех шаговых управлений: U =(U1, U2,…Um). Управление может удовлетворительным и неудовлетворительным, оно может быть эффективным или неэффективным. Как правило, эффективность управления оценивается при помощи того же самого показателя IV, что и эффективность самой операции в целом. В рассматриваемом нами примере показатель эффективности операции (целевая функция задачи) выражается как суммарный доход от всего комплекса предприятий за определенное количество (т) лет. Величина этого показателя зависит от качества управления за весь период времени U, т.е. от всей совокупности пошаговых управлений: W = W(U) = W(U1, U2,..,Um). Возникает вопрос: как выбрать пошаговые управления U1 U2, Um, чтобы величина показателя эффективности была наибольшей (максимальной) из всех возможных? Поставленная таким образом проблема называется задачей оптимизации управления, а управление, при котором показатель становится максимальным, носит название оптимального управления. В дальнейшем мы будем обозначать оптимальное управление (в отличие от управления в общем случае U) буквой и. Таким образом, оптимальное управление и многошаговым процессом состоит из совокупности оптимальных шаговых управлений: u = (u1,и2…,ит). Задача оптимизации управления выглядит следующим образом: определить оптимальное управление на каждом шаге процесса ui (i= 1, 2, т) и, следовательно, оптимальное управление всей операцией. Заметим, что в рассматриваемом нами примере (управление распределением финансовых средств группы предприятий) показатель эффективности представляет собой сумму доходов за все отдельные годы исследуемого периода времени: W = w1 + w2 + … + wm где w, — доход от всей системы за год i. Показатель, обладающий таким свойством, называется аддитивным. Задание 5 Ситуация для анализа «Решение Джилетта» Кинг Кэмп Джиллетт пошел по стопам отца, т.е. стал работать по части скобяных товаров. В 21 год он был уже не клерком, а разъездным представителем фирмы. Во время поездок Кинг придумывал разные изобретения. В 1879 г. он запатентовал комплект из поршня и втулки для водопроводного крана, через десять лет получил патент на два новых типа электрических проводников. Ни одно из его изобретений не принесло ему материальных благ, но он продолжал свою новаторскую деятельность. Один из его хозяев оценил торговые способности Джиллетта и понял тягу молодого человека к изобретательству. Босса звали Уильям Пэйнтер, он был президентом Балтиморской компании по производству сальников и уплотнителей и тоже любил изобретать. Одним из доходных изобретений Пэйнтера был вентиль из мягкой резины для очистки выгребных ям и уборных. Но самым замечательным изобретением, сделавшим его очень богатым человеком, была металлическая корончатая бутылочная пробка с прокладкой, которой мы пользуемся и сегодня. Пэйнтер сделал сорокалетнего Джиллетта своим протеже и другом, а в 1885 г. дал совет: «Кинг, не попробовать ли тебе изобрести что-то вроде моей пробки, которую после использования выбрасывают? Чтобы покупатель приходил за новой пробкой. Ведь каждая покупка будет обогащать тебя». Кинг стал думать. Он тщательно изучал словарь, выискивая предметы, нужные людям, но так и не смог найти вещь, которую человек захотел бы выбросить после одноразового использования. Как-то утром во время умывания в ванной комнате гостиничного номера Джиллетт заметил, что его бритва затупилась. Это означало, что бритву надо отнести парикмахеру или точильщику для заточки, правки и доводки. Он стоял с бритвой в руке в глубокой задумчивости. И тут ему пришло в голову, что конструкцию бритвы не меняли уже несколько столетий. А если бы появилась возможность сделать бритвенные лезвия такими дешевыми, чтобы их не затачивать и не править, а просто выбрасывать и заменять новыми? Так родились на свет бритвенные станки «Джиллетт». Потребовалось еще восемь лет на разработку всех деталей станка, а также помощь инженера по имени Уильям Никерсон. Опытные специалисты сказали, что замысел Джиллетта неосуществим, но тот не желал об этом слушать, он испытывал все новые и новые металлы и сплавы, различные модели корпусов и рукояток. Наконец в 1903 г. началось серийное производство бритв. В тот год компания смогла продать только 51 бритвенный станок и 168 лезвий. Джиллетт продолжал работать разъездным агентом фирмы пробок и уплотнителей. В сентябре 1903 г. его послали в деловую поездку в Англию, предложив такую хорошую оплату, что он не смог отказаться от командировки. Он переплыл океан, неохотно оставив свою фирму «Бритвы Джиллетта» на попечение Совета директоров. После отъезда Джиллетта фирма практически начала разоряться, и Совет решил распродать акции и покончить с делом. Но тут показатели продаж неожиданно поползли вверх. О бритвенных станках стали хорошо отзываться в прессе. В 1904 г. компания распродала 91 000 бритвенных станком и 123 000 лезвий. В ноябре 1904 г. Джиллетт бросил работу коммивояжера и вернулся в Штаты. Сегодня бритвенные станки «Джиллетт» используются миллионами потребителей по всему миру. 1 Проанализируйте ситуации. Сформулируйте объект, предмет, проблему и условия приятия решений. Предмет – создание нового уникального товара на рынке. Объект – процесс разработки и выхода на рынок нового продукта в виде одноразового бритвенного станка и сменных лезвий. 2 Выявите экономический, организационный, социальный, правовой, технологический, психологический аспекты представленных решений.Технологический и организационные аспект заключались в испытании и поиске сплава, оптимального и безопасного для одноразового использования. Экономический аспект – затраты на разработку, определение себестоимости станка. Для компании производство и дальнейшая реализация должны быть экономически выгодными.