1. Выбор варианта производится по последней цифре номера зачетной книжки студента:

 

Последняя цифра номера зачетной книжки	Номер варианта	Номера задач
1	1	1, 11, 21, 31, 41, 51, 61, 71
2	2	2, 12, 22, 32, 42, 52, 62, 72
3	3	3, 13, 23, 33, 43, 53, 63, 73
4	4	4, 14, 24, 34, 44, 54, 64, 74
5	5	5, 15, 25, 35, 45, 55, 65, 75
6	6	6, 16, 26, 36, 46, 56, 66, 76
7	7	7, 17, 27, 37, 47, 57, 67, 77
8	8	8, 18, 28, 38, 48, 58, 68, 78
9	9	9, 19, 29, 39, 49, 59, 69, 79
0	10	10, 20, 30, 40, 50, 60, 70, 80

 

2. Титульная страница оформляется согласно нижеследующему образцу (см. стр. 3).

 

3. Студенты заочной традиционной формы обучения выполняют работу в рукописном виде в отдельной тетради (ученическая тетрадь в клетку, 12 листов) или в печатном виде на листах формата А4 (расположение номера страницы – внизу по центру, титульная страница не ну- меруется).

 

4. Студенты заочной дистанционной формы обучения выполняют работу в электронном виде (формат страниц А4). Рекомендуем текстовый редактор Microsoft Word, набор формул в Microsoft Equation 3.0. Если испытываете затруднения с компьютерным набором, то, в по- рядке исключения, можете выполнить работу в рукописном виде и отправить на проверку скан–копию работы.

 

5. В начале решения каждой задачи должно быть приведено общее условие задания с данны- ми из своего варианта. Преподаватель имеет право не проверять решение задачи, если усло- вие задачи отсутствует, при этом он может не зачесть работу и отправить её студенту на до- работку.

 

6. В конце контрольной работы студент приводит список использованной литературы (с ука- занием страниц).

 

7. Студенты заочной традиционной формы обучения присылают или приносят выполненную контрольную работу методистам заочного факультета или приносят непосредственно на ка- федру «Высшая математика» (аудитория 401-л).

 

8. Студентам запрещено вносить исправления в проверенную контрольную работу. В случае замечаний преподавателя исправления ошибок добавляются в конце работы после списка использованной литературы.

   Образец оформления титульной страницы контрольной работы.      

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

 

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Тихоокеанский государственный университет» Кафедра «Высшая математика»

 

 

КОНТРОЛЬНАЯ РАБОТА № 1

 

по дисциплине «МАТЕМАТИКА»

     

Вариант (номер варианта)

       

Выполнил(а)

 

Студент(ка) (Фамилия И. О.)

Группа (Название учебной группы)

Шифр (Номер зачетной книжки)

 

Хабаровск (Год выполнения контрольной работы)

 

1.  Классическое определение вероятности

1. В отделе работают 8 аудиторов, из которых 3 высокой квалификации. В команди- ровку необходимо отправить группу из 4 человек. Какова вероятность того, что в этой группе окажется только один аудитор высокой квалификации, если каждый специалист име- ет равные возможности поехать в командировку?
2. В группе из 30 студентов 5 имеют спортивные разряды. Из этой группы наугад вы- браны 3 студента. Найти вероятность того, что все они имеют спортивные разряды.
3. В ящике 10 красных и 5 синих пуговиц. Одновременно (случайным образом) выни- мают две пуговицы. Какова вероятность того, что пуговицы будут разных цветов?
4. В магазине 8 продавцов, из них 5 женщин. В каждую смену заняты три продавца. Какова вероятность того, что в наудачу выбранную смену все три продавца будут женщины?
5. В ящике лежат 10 заклепок, среди них 5 железных, 3 латунных и 2 медных. Найти вероятность того, что из трех вынутых наудачу заклепок одна будет железной, две другие медными.
6. В классе из 20 человек 4 имеют одинаковые имена. Найти вероятность того, что сре- ди наудачу отобранных пяти человек двое будут с одинаковыми именами.
7. Библиотекарь наудачу выбирает две книги из 15 книг по математике. Какова вероятность того, что эти книги одного автора, если таких книг всего три?
8. В коробке 12 одинаковых по виду ручек: 8 с синей пастой и 4 с чёрной. Наугад берут 4 ручки. Определить вероятность, что среди них будет 2 ручки с синей пастой и 2 с чёрной.
9. В коробке 25 конфет, 10 из них с орехами. Найти вероятность, что из трех случайно взятых конфет две с орехами?
10. Среди 8 задач, предлагаемых для решения, 3 считаются трудными. Студенту пред- лагается наудачу 4 задачи. Найти вероятность того, что среди них окажется одна трудная.

 

2.  Сложение и умножение вероятностей

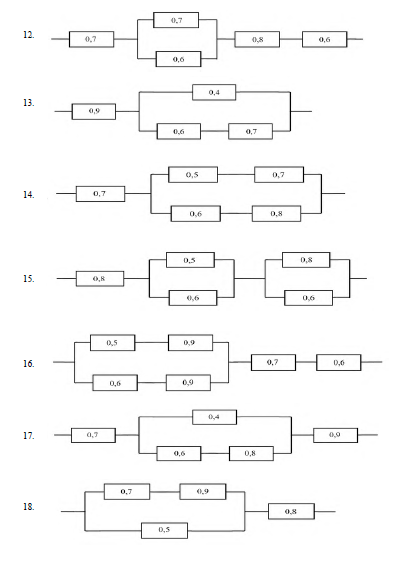
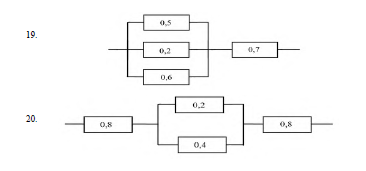
11-20. Имеется система соединенных между собой элементов. Надежность (вероятность работы) каждого элемента указана. Найти вероятность безотказной работы всей системы.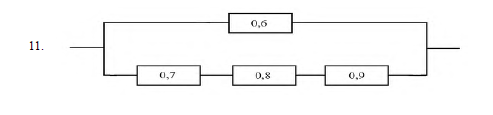

1.  Схема Бернулли

21. Посадили 8 сортовых тюльпанов. Вероятность того, что каждый тюльпан взойдет, равна 0,8. Найти вероятность того, что из посаженных тюльпанов взойдет только
22. Вратарь в среднем пропускает один мяч из пяти. Какова вероятность того, что из четырех ударов по воротам будет пропущен только один мяч?
23. На заочном отделении вуза 40% всех студентов работают по специальности. Како- ва вероятность того, что из пяти отобранных случайным образом студентов по специально- сти работают три?
24. При вытачивании болтов в среднем наблюдается 10% брака. Какова вероятность то- го, что среди шести случайно отобранных болтов будет два бракованных?
25. Вероятность того, что менеджер фирмы находится в командировке в данный мо- мент, равна 0,7. Найти вероятность того, что из пяти менеджеров фирмы в данный момент в командировке находятся два менеджера.
26. Аудитор обнаруживает финансовые нарушения у проверяемой фирмы с вероятностью 0,9. Найти вероятность того, что среди 4 проверенных фирм нарушения будут выявлены только у одной.
27. Вероятность того, что к 15 апреля машина не прошла техосмотр, равна 0,3. Какова вероятность что из 6 случайно выбранных машин техосмотр к данному числу не прошли
28. В рекламных целях торговая фирма вкладывает приз в каждую десятую единицу товара. Какова вероятность того, что покупатель, сделав три покупки, получит один приз.
29. Вероятность поступления рекламации на предприятие в течение месяца равна 0,2. Найти вероятность того, что в течение пяти месяцев не будет ни одной рекламации.
30. Вероятность выхода на линию в течение определенного дня каждого из пяти авто- бусов некоторого коммерческого предприятия равна 0,9. Найти вероятность того, что в определенный день на линию выйдут три автобуса этого предприятия.

 

2.  Предельные теоремы в схеме Бернулли

 

31. Доля кислых яблок составляет 40%. от общего числа. Какова вероятность взяв 50 яблок обнаружить среди них: а) 22 кислых; б) от 15 до 20 кислых?
32. Вероятность того, что при одном измерении будет допущена ошибка, равна 0,01. Найти вероятность того, что из 200 произведённых измерений будет не более 2 ошибочных.
33. Вероятность выхода из строя за некоторое время Т одного конденсатора равна 0,1. Найти вероятность того, что из 100 конденсаторов в течение времени Т из строя выйдут:

а) ровно 17 конденсаторов; б) от 4 до 19 конденсаторов.

34. Вероятность того, что фотография окажется некачественной, равна 0,07. Найти вероятность, что из 100 отобранных наугад фотографий некачественных будет не более
35. Каждый из студентов группы посещает занятия по математике с вероятность 0,9. Найти вероятность того, что в группе из 30 студентов на очередном занятии будет присутствовать: а) 25 студентов; б) от 20 до 30 студентов.
36. Ежемесячно 1% компаний одного профиля прекращают свою деятельность по при- чине низкой конкурентоспособности. Определить вероятность того, что из 100 компаний одного профиля в последний месяц прекратило свою деятельность не более 3?
37. Штамповка металлических клемм для пластин дает 90 % стандартных клемм. Опре- делить вероятность того, что в партии из 500 клемм будет стандартных: а) от 425 до 460 клемм; б) равно 470 клемм.
38. Допустим, что вероятность случайно встретить на улице знакомого, равна 0,005. Найти вероятность того, что среди 1000 случайных прохожих Вы встретите не более двух знакомых.
39. Страховая компания заключила 400 договоров. Вероятность страхового случая по каждому из них в течение года составляет 2%. Найти вероятность, что в течение года страховых случаев будет не менее 2.
40. В среднем шестая часть акций на аукционах продаётся по первоначально заявлен- ной цене. Найти вероятность того, что из 120 пакетов акций в результате торгов по первоначально заявленной цене будет продано: а) 30 пакетов; б) от 25 до 40 пакетов.

 

3.  Закон распределения дискретной случайной величины

41. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения случайной вели-

  чины X – числа отказа элементов в одном опыте. Найти M ( X ) , D( X ) и d ( X ) .  

42. В партии из 6 деталей, имеется 4 стандартных. Наудачу отобраны 3 детали. Соста- вить закон распределения случайной величины X – числа стандартных деталей среди ото-

  бранных. Найти M ( X ) , D( X ) , d ( X ) .  

43. Вероятность попадания в цель из орудия равна 0,8. Составить закон распределения

случайной величины X – числа попаданий в трех выстрелах. Найти M ( X ) , D( X ) , d ( X ) .

44. Вероятность того, что саженец яблони приживется, равна 0,7. Посажены 3 саженца. Составить закон распределения случайной величины X – числа прижившихся саженцев.

  Найти M ( X ) , D( X ) , d ( X ) .  

45. В партии деталей содержится 20 % нестандартных. Составить закон распределения случайной величины X – числа нестандартных деталей среди двух отобранных. Найти

  M ( X ) , D( X ) , d ( X ) .  

46. В коробке среди 5 карандашей 3 черных. Наугад берут 2 карандаша. Составить закон распределения случайной величины X – числа черных карандашей среди отобранных.

  Найти M ( X ) , D( X ) , d ( X ) .  

47. Экзаменационный билет содержит 3 вопроса. Вероятность того, что данный студент ответит на вопрос билета, равна 0,8. Составить закон распределения случайной величины X

  – числа вопросов, на которые правильно ответит студент. Найти M ( X ) , D( X ) , d ( X ) .  

48. Известно, что в определенном городе 30 % горожан добираются на работу личным автотранспортом. Случайно выбраны 2 человека. Составить закон распределения случайной величины X – числа людей, добирающихся на работу личным автотранспортом. Найти

  M ( X ) , D( X ) , d ( X ) .  

49. В стопке из 7 книг 4 книги по математике и 3 по информатике. Выбирают наудачу три книги. Составить закон распределения случайной величины X – числа книг по матема-

  тике среди отобранных. Найти M ( X ) , D( X ) , d ( X ) .  

50. В партии из 8 изделий 3 имеют скрытые дефекты. Наугад выбраны 2 изделия. Составить закон распределения случайной величины X – числа деталей, имеющих скрытые

  дефекты, среди двух отобранных. Найти числовые характеристики M ( X ) , D( X ) и d ( X ) .

6.  Непрерывная случайная величина

7.  Нормальное распределение

 

61. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = 1 и дисперсией D(X) = Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(-3 < X £ 6); б) P(| X — 1| < 8).
62. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = 6 и дисперсией D(X) = 1,44. Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(4 < X £ 7); б) P(| X — 6| < 3).
63. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = – 5 и дисперсией D(X) = 0,64. Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(– 6 < X £ – 3);

б) P(| X + 5| < 0,7).  

64. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = – 3 и дисперсией D(X) = Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(– 4 £ X < 1); б) P(| X + 3| < 11).
65. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = 6 и дисперсией D(X) = Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(2 £ X £ 13); б) P(| X — 6| < 3).
66. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = 2 и дисперсией D(X) = 0,81. Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(2 £ X £ 4); б) P(| X + 2| < 1).
67. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = 3 и дисперсией D(X) = Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(1 £ X £ 6); б) P(| X — 3| < 9).
68. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = – 2 и дисперсией D(X) = 0,25. Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(– 4 £ X < –1);

б) P(| X + 2| < 0,3).

69. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = – 1 и дисперсией D(X) = Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(0 £ X < –7); б) P(| X + 1| < 21).
70. Случайная величина X распределена по нормальному закону с математическим ожиданием M(X) = 4 и дисперсией D(X) = 0,36. Записать и схематически построить график функции плотности вероятности f(x). Найти вероятности: а) P(2 £ X £ 5); б) P(| X — 4| < 1).