Автор статьи

Валерия
Эксперт по сдаче вступительных испытаний в ВУЗах
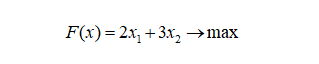 Тогда ограничения по выделенному числу денежных средств, по имеющейся площади размещения и приобретению не более 8 машин типа В:
Также заметим, что должны быть целыми.
Решим задачу средствами Microsoft Excel:
В режиме показа формул:
Получили решение:
Таким образом, необходимо приобрести 2 машины типа А и 7 машин типа B. При этом максимальная общая производительность составит 25 т зерна за смену.
Заметим, что денежные средства использованы полностью, а из площади помещения в 60 кв. м машинами занято только 41 кв. м.
Цель работы
Изучение процесса составления математических моделей прикладных задач. Постановка транспортной задачи (ТЗ). Методы северо-западного угла и минимального элемента для поиска начального опорного решения. Решение транспортной задачи методом потенциалов.
Задание: Построить математическую модель задачи. Номер задачи соответствует номеру студента в списке группы. Студент с номером 13 делает задачу №1 и т.д.
Изучить процесс решения ТЗ (см. теоретическую часть данной работы). Решить задачу своего варианта методом потенциалов. Начальное опорное решение найти методом минимального элемента. Возможна реализация проверки полученного решения с применением надстройки Поиск решения в MS Excel (при необходимости).
Решение:
Матрица тарифов имеет вид
Общий объем поставок производителей ∑▒a_i =60+40+100+50=250 равен суммарной потребности потребителей ∑▒b_i =30+80+65+35+40=250, т.е. имеем закрытую модель транспортной задачи.
Найдем начальное решение методом минимального элемента.
Минимальный элемент матрицы тарифов находится в ячейке A4B3 и равен 2, т.е. из незадействованных маршрутов, маршрут доставки продукции от поставщика A4 к потребителю B3 наиболее рентабельный. Запасы поставщика A4 составляют 50 единиц продукции. Потребность потребителя B3 составляет 65 единиц продукции. Разместим в ячейку A4B3 значение равное 50. Мы полностью израсходовали запасы поставщика A4.
Далее аналогично:
От поставщика A2 к потребителю B4 будем доставлять min = {40, 35} = 35 единиц продукции. Мы полностью удовлетворили потребность потребителя B4.
От поставщика A1 к потребителю B3 будем доставлять min = {60, 15} = 15 единиц продукции. Мы полностью удовлетворили потребность потребителя B3.
От поставщика A3 к потребителю B2 будем доставлять min = {100, 80} = 80 единиц продукции. Мы полностью удовлетворили потребность потребителя B2.
От поставщика A2 к потребителю B5 будем доставлять min = {5, 40} = 5 единиц продукции. Мы полностью израсходовали запасы поставщика A2.
От поставщика A3 к потребителю B5 будем доставлять min = {20, 35} = 20 единиц продукции. Мы полностью израсходовали запасы поставщика A3.
От поставщика A1 к потребителю B1 будем доставлять min = {45, 30} = 30 единиц продукции. Мы полностью удовлетворили потребность потребителя B1.
От поставщика A1 к потребителю B5 будем доставлять min = {15, 15} = 15 единиц продукции. Мы полностью удовлетворили потребность потребителя B5. Мы полностью израсходовали запасы поставщика A1.
Начальный план:
Заполненные ячейки — базисные, остальные — свободные. Для решения задачи методом потенциалов, количество базисных ячеек (задействованных маршрутов) должно равняться m + n — 1, где m — количество строк в таблице, n — количество столбцов в таблице. Количество базисных ячеек равно 8, что и требуется для невырожденности опорного плана.
Оценим полученное решение. Имеем 8 линий поставок и 9 общих потенциалов, следовательно, 1 потенциал можно определить произвольно, например u1=0. Для занятых клеток необходимо, чтобы стоимость соответствующих перевозок cij удовлетворяла равенству: ui + vi = cij,
Поставщик Потребитель Запас U
Найдем оценки незадействованных маршрутов (для свободных клеток):
E_ij=с_ij-(u_i+v_j)
Оценки свободных ячеек E_ij определяются как стоимость доставки с_ij минус сумма соответствующих потенциалов. Оценка свободной клетки E_ij показывает, насколько увеличатся суммарные расходы по перевозке груза, если поставить единицу груза от i-го производителя j-му потребителю (перераспределив остальные поставки так, чтобы сохранился баланс по строкам и столбцам). Найдём E_ij
Среди оценок свободных ячеек есть отрицательные, выбираем минимальную оценку и для данной ячейки (A4B5) строим цикл пересчёта (4,5 → 4,3 → 1,3 → 1,5). Можно перераспределить 15 единиц продукции
Поставщик Потребитель Запас
Оценим полученное решение, 1 потенциал можно определить произвольно, например u1=0.
Поставщик Потребитель Запас U
Найдем оценки незадействованных маршрутов (для свободных клеток):
E_ij=с_ij-(u_i+v_j)
Среди оценок свободных ячеек есть отрицательные, выбираем одну из минимальных оценок и для данной ячейки (A2B1) строим цикл пересчёта ((2,1 → 2,5 → 4,5 → 4,3 → 1,3 → 1,1). Можно перераспределить 5 единиц продукции.
Поставщик Потребитель Запас
Оценим полученное решение, 1 потенциал можно определить произвольно, например u1=0.
Поставщик Потребитель Запас
Найдем оценки незадействованных маршрутов (для свободных клеток):
Среди оценок свободных ячеек есть отрицательная (A4B1) строим цикл пересчёта (4,1 → 4,3 → 1,3 → 1,1). Можно перераспределить 25 единиц продукции.
Поставщик Потребитель Запас
Оценим полученное решение, 1 потенциал можно определить произвольно, например u1=0.
Поставщик Потребитель Запас U
Найдем оценки незадействованных маршрутов (для свободных клеток):
E_ij=с_ij-(u_i+v_j)
Данный план является оптимальным, поскольку все оценки свободных клеток неотрицательны.
Оптимальный план перевозок:
Производители Потребители Запасы
Минимальные затраты:
Smin = 4*60 + 7*5 + 3*35 + 4*80 + 7*20 + 5*25 + 2*5 + 4*20 = 1055 (ден.ед)
Цель работы
Решение прикладных задач с применением вероятностного подхода
Задание: Каждый студент должен решить 1 задачу из списка задач по непрерывным случайным величинам (см. стр. 5) и 1 задачу из списка по дискретным случайным величинам (см. стр. 9) (всего каждый решает две задачи). Номера задач в списках соответствует номеру студента в списке группы.
Задача 1
Число зданий, обрушившихся в результате землетрясения, является непрерывной случайной величиной. Функция распределения случайной величины имеет вид
F(x)={■(0,x<5@〖(x-1)〗^2,@1,x>10)┤5≤x≤10
Найти M(Х), D(X), P(6≤x≤9).
Решение:
Поскольку случайная величина непрерывная, то функция распределения также должна быть непрерывна, поэтому
lim┬(x⟶5-0)F(x)=0
lim┬(x⟶5+0)F(x)=lim┬(x⟶5+0)〖〖(x-1)〗^2 〗=16
lim┬(x⟶5-0)F(x)≠lim┬(x⟶5+0)F(x)
Т.е. в точке x=5 функция терпит разрыв. Также по свойствам функции распределения 0≤F(x)≤1, поскольку имеет смысл вероятности F(x)=P(X<x).
Ответ: данная функция F(x) не является функцией распределения для непрерывных случайных величин, так как терпит разрыв и её значение превышает единицу на области определения.
Тогда ограничения по выделенному числу денежных средств, по имеющейся площади размещения и приобретению не более 8 машин типа В:
Также заметим, что должны быть целыми.
Решим задачу средствами Microsoft Excel:
В режиме показа формул:
Получили решение:
Таким образом, необходимо приобрести 2 машины типа А и 7 машин типа B. При этом максимальная общая производительность составит 25 т зерна за смену.
Заметим, что денежные средства использованы полностью, а из площади помещения в 60 кв. м машинами занято только 41 кв. м.
Цель работы
Изучение процесса составления математических моделей прикладных задач. Постановка транспортной задачи (ТЗ). Методы северо-западного угла и минимального элемента для поиска начального опорного решения. Решение транспортной задачи методом потенциалов.
Задание: Построить математическую модель задачи. Номер задачи соответствует номеру студента в списке группы. Студент с номером 13 делает задачу №1 и т.д.
Изучить процесс решения ТЗ (см. теоретическую часть данной работы). Решить задачу своего варианта методом потенциалов. Начальное опорное решение найти методом минимального элемента. Возможна реализация проверки полученного решения с применением надстройки Поиск решения в MS Excel (при необходимости).
Решение:
Матрица тарифов имеет вид
Общий объем поставок производителей ∑▒a_i =60+40+100+50=250 равен суммарной потребности потребителей ∑▒b_i =30+80+65+35+40=250, т.е. имеем закрытую модель транспортной задачи.
Найдем начальное решение методом минимального элемента.
Минимальный элемент матрицы тарифов находится в ячейке A4B3 и равен 2, т.е. из незадействованных маршрутов, маршрут доставки продукции от поставщика A4 к потребителю B3 наиболее рентабельный. Запасы поставщика A4 составляют 50 единиц продукции. Потребность потребителя B3 составляет 65 единиц продукции. Разместим в ячейку A4B3 значение равное 50. Мы полностью израсходовали запасы поставщика A4.
Далее аналогично:
От поставщика A2 к потребителю B4 будем доставлять min = {40, 35} = 35 единиц продукции. Мы полностью удовлетворили потребность потребителя B4.
От поставщика A1 к потребителю B3 будем доставлять min = {60, 15} = 15 единиц продукции. Мы полностью удовлетворили потребность потребителя B3.
От поставщика A3 к потребителю B2 будем доставлять min = {100, 80} = 80 единиц продукции. Мы полностью удовлетворили потребность потребителя B2.
От поставщика A2 к потребителю B5 будем доставлять min = {5, 40} = 5 единиц продукции. Мы полностью израсходовали запасы поставщика A2.
От поставщика A3 к потребителю B5 будем доставлять min = {20, 35} = 20 единиц продукции. Мы полностью израсходовали запасы поставщика A3.
От поставщика A1 к потребителю B1 будем доставлять min = {45, 30} = 30 единиц продукции. Мы полностью удовлетворили потребность потребителя B1.
От поставщика A1 к потребителю B5 будем доставлять min = {15, 15} = 15 единиц продукции. Мы полностью удовлетворили потребность потребителя B5. Мы полностью израсходовали запасы поставщика A1.
Начальный план:
Заполненные ячейки — базисные, остальные — свободные. Для решения задачи методом потенциалов, количество базисных ячеек (задействованных маршрутов) должно равняться m + n — 1, где m — количество строк в таблице, n — количество столбцов в таблице. Количество базисных ячеек равно 8, что и требуется для невырожденности опорного плана.
Оценим полученное решение. Имеем 8 линий поставок и 9 общих потенциалов, следовательно, 1 потенциал можно определить произвольно, например u1=0. Для занятых клеток необходимо, чтобы стоимость соответствующих перевозок cij удовлетворяла равенству: ui + vi = cij,
Поставщик Потребитель Запас U
Найдем оценки незадействованных маршрутов (для свободных клеток):
E_ij=с_ij-(u_i+v_j)
Оценки свободных ячеек E_ij определяются как стоимость доставки с_ij минус сумма соответствующих потенциалов. Оценка свободной клетки E_ij показывает, насколько увеличатся суммарные расходы по перевозке груза, если поставить единицу груза от i-го производителя j-му потребителю (перераспределив остальные поставки так, чтобы сохранился баланс по строкам и столбцам). Найдём E_ij
Среди оценок свободных ячеек есть отрицательные, выбираем минимальную оценку и для данной ячейки (A4B5) строим цикл пересчёта (4,5 → 4,3 → 1,3 → 1,5). Можно перераспределить 15 единиц продукции
Поставщик Потребитель Запас
Оценим полученное решение, 1 потенциал можно определить произвольно, например u1=0.
Поставщик Потребитель Запас U
Найдем оценки незадействованных маршрутов (для свободных клеток):
E_ij=с_ij-(u_i+v_j)
Среди оценок свободных ячеек есть отрицательные, выбираем одну из минимальных оценок и для данной ячейки (A2B1) строим цикл пересчёта ((2,1 → 2,5 → 4,5 → 4,3 → 1,3 → 1,1). Можно перераспределить 5 единиц продукции.
Поставщик Потребитель Запас
Оценим полученное решение, 1 потенциал можно определить произвольно, например u1=0.
Поставщик Потребитель Запас
Найдем оценки незадействованных маршрутов (для свободных клеток):
Среди оценок свободных ячеек есть отрицательная (A4B1) строим цикл пересчёта (4,1 → 4,3 → 1,3 → 1,1). Можно перераспределить 25 единиц продукции.
Поставщик Потребитель Запас
Оценим полученное решение, 1 потенциал можно определить произвольно, например u1=0.
Поставщик Потребитель Запас U
Найдем оценки незадействованных маршрутов (для свободных клеток):
E_ij=с_ij-(u_i+v_j)
Данный план является оптимальным, поскольку все оценки свободных клеток неотрицательны.
Оптимальный план перевозок:
Производители Потребители Запасы
Минимальные затраты:
Smin = 4*60 + 7*5 + 3*35 + 4*80 + 7*20 + 5*25 + 2*5 + 4*20 = 1055 (ден.ед)
Цель работы
Решение прикладных задач с применением вероятностного подхода
Задание: Каждый студент должен решить 1 задачу из списка задач по непрерывным случайным величинам (см. стр. 5) и 1 задачу из списка по дискретным случайным величинам (см. стр. 9) (всего каждый решает две задачи). Номера задач в списках соответствует номеру студента в списке группы.
Задача 1
Число зданий, обрушившихся в результате землетрясения, является непрерывной случайной величиной. Функция распределения случайной величины имеет вид
F(x)={■(0,x<5@〖(x-1)〗^2,@1,x>10)┤5≤x≤10
Найти M(Х), D(X), P(6≤x≤9).
Решение:
Поскольку случайная величина непрерывная, то функция распределения также должна быть непрерывна, поэтому
lim┬(x⟶5-0)F(x)=0
lim┬(x⟶5+0)F(x)=lim┬(x⟶5+0)〖〖(x-1)〗^2 〗=16
lim┬(x⟶5-0)F(x)≠lim┬(x⟶5+0)F(x)
Т.е. в точке x=5 функция терпит разрыв. Также по свойствам функции распределения 0≤F(x)≤1, поскольку имеет смысл вероятности F(x)=P(X<x).
Ответ: данная функция F(x) не является функцией распределения для непрерывных случайных величин, так как терпит разрыв и её значение превышает единицу на области определения.
Задача 2
Производятся последовательные испытания пяти приборов на надежность. Каждый следующий испытывается только в том случае, если предыдущий оказался надежным. Построить ряд распределения случайного числа испытаний приборов, найти М(Х), D(Х), если вероятность выдержать испытание для каждого из них равна 0,85. Решение: Если испытан только один прибор, то первый же проверенный оказался ненадёжным: P(X=1)=1-0.85=0.15 Если испытано 2 прибора, то первый оказался надёжным, а второй нет: P(X=2)=0.85∙0.15=0.1275 Если испытано 3 прибора, то первые два оказались надёжными, а третий нет: P(X=3)=〖0.85〗^2∙0.15=0.108375 Если испытано 4 прибора, то первые три оказались надёжными, а четвёртый нет: P(X=4)=〖0.85〗^3∙0.15=0.09211875 Если испытано все 5 приборов, то первые четыре оказались надёжными, надёжность пятого не важна, так как он последний: P(X=5)=〖0.85〗^4=0.52200625 Ряд распределения будет иметь вид: Математическое ожидание M(X)=∑_(i=1)^5▒〖x_i p_i 〗=1∙0.15+2∙0.1275+3∙0.108375+4∙0.09211875+ +5∙0.52200625=3.70863125 Дисперсия D(X)=M(X^2)-〖(M(X))〗^2 M(X^2)=∑_(i=1)^5▒〖x_i^2 p_i 〗=1∙0.15+4∙0.1275+9∙0.108375+16∙0.09211875+ +25∙0.52200625=16.15943125 D(X)=16.15943125-〖3.70863125〗^2≈2.4054855 Ответ: M(X)=3.70863125;D(X)≈2.4054855. Цель работы Решение прикладных задач с применением законов распределения случайных величин. Нормальный, показательный законы. Задание: Каждый студент должен решить 1 задачу из списка задач по нормальному закону распределения (см. стр. 7) и 1 задачу из списка по показательному закону (см. стр. 12) (всего каждый решает две задачи). Номера задач в списках соответствует номеру студента в списке группы.Задача 1
Образцы из прессованного дюралюминиевого профиля испытывают на разрыв с целью определения предела прочности. Определить вероятность попадания значения предела прочности испытываемого образца в интервал (50кгс/мм2; 55 кгс/мм2), если для случайной величины Х равной пределу прочности бетона известно, что a= 51 кгс/мм2, среднее квадратичное равно 1,13 кгс/мм2. Решение: Вероятность попадания нормально распределенной случайной величины интервал (x_1;x_2) определяется по формуле: P(x_1<x5 .Значения функции находим из таблиц. Имеем a=51,σ=1.13. Получаем: P(50<x<55)=Φ((55-51)/1.13)-Φ((50-51)/1.13)≈Φ(3.54)-Φ(-0.88)= =Φ(3.54)+Φ(0.88)≈0.4998+0.3106=0.8104. Ответ: 0.8104. Задача 2 Время безотказной работы элемента распределено по показательному закону со средним временем до первого отказа 60 часов. Найти вероятность того, что элемент проработал 150 часов. Решение: Вероятность того, что элемент проработал t часов определяется по формуле P(T>t)=1-F(t)=e^(-λt). Поскольку известно, что средне время до первого отказа 60 часов, т.е. M(X)=60 ч, то M(X)=1/λ, значит λ=1/M(X) =1/60 ч^(-1). Находим: P(T>150)=e^(-150/60)=e^(-2.5)≈0.0821. Ответ: 0.0821. Цель работы Целью работы является приобретение навыков по расчету и анализу основных характеристик систем массового обслуживания. Задание: Для задачи из списка построить граф состояний системы. Определить характеристики работы системы. Сделать соответствующие выводы по дальнейшему функционированию СМО. Задача: В методическом отделе управления институтом три телефонные линии. В среднем в отдел поступает 60 звонков в час. Среднее время переговоров составляет 10 мин. Определите основные характеристики СМО, оцените ее работу. (многоканальная СМО с отказами) Решение: Строим граф состояний системы: S_0 — все телефонные линии свободны; S_1 — занята одна телефонная линия; S_2 — занято две телефонные линии; S_2 — все три телефонные линии заняты; λ=60(звонков/час) Среднее время переговоров составляет 10 мин, т.е. 1/6 часа. Тогда интенсивность обслуживания на одного оператора: μ=1/(1/6)=6 (звонков/час) Коэффициент загрузки ρ=λ/μ=10 По формуле Эланга находим вероятность того, что все каналы свободны: p_0=(1+ρ/1!+ρ^2/2!+ρ^3/3!)^(-1)=(1+10+100/2+1000/6)^(-1)=3/683≈0.0044 Вероятность отказа P_отк=ρ^3/3!∙p_0=0.7321 Относительная пропускная способность находится по формуле Q=1-P_отк=0.2679 Абсолютная пропускная способность A=λ∙Q=60∙0.2679=16.076 звонков в час Среднее число занятых линий связи n ̅_з=A/μ=16.076/6=2.679 Коэффициент загрузки K_заг=K_з=n ̅_з/n=2.679/3=0.893 Таким образом, при загрузке СМО на 89,3% будет обработано в среднем 16.08 звонков за час, отказ получат 73,21% вызовов. Т.е. обслуживание очень неэффективное, рекомендуется добавить в СМО дополнительное число каналов обслуживания (телефонных линий). Цель работы: Целью работы является приобретение навыков решения статистических игр ЛПР с природой в условиях неопределенности, используя различные критерии принятия решений. Задание: Машину (станок, технологическую установку, конвейер и т.п.) требуется подвергнуть проверке с приостановкой ее эксплуатации и выпуска продукции. Вовремя не обнаруженная неисправность может привести к капитальной поломке машины. У ЛПР имеется три варианта решения: E1 — полная проверка; Е2 — минимальная проверка; Е3 — отказ от проверки. Машина может находиться в следующих состояниях: F1 — исправна; F2 — незначительная неисправность; F3 — серьезная неисправность. Необходимо найти оптимальное решение ЛПР по MM-, S-, НW-, Р-, BL-, HL-, G-критериям. Для заданной матрицы выигрыша из списка найти оптимальное решение ЛПР по перечисленным выше критериям, если вероятности состояний спроса: 0,2; 0,5; 0,3; коэффициент пессимизма λ = 0,4; коэффициент достоверности информации о состояниях спроса u = 0,6. Исходные данные: Решение: Минимаксный критерий MM Выбираем максимальный элемент Z_MM=max┬imin┬j〖e_ij 〗 =max{-20;-12;-15}=-12 По данному критерию следует выбрать стратегию E_2. Это решение полностью исключает риск. Критерий Севиджа S Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается: A=min┬imax┬j〖r_ij 〗 Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации. Находим матрицу рисков. Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Выбираем минимальный элемент Z_S=min┬imax┬j〖r_ij 〗 =min{17;12;7}=7 По данному критерию следует выбрать стратегию E_3. Критерий Гурвица НW Критерий Гурвица является критерием пессимизма — оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение (примем λ=0.4): Z_НW=max〖(λ min〖e_ij 〗+(1-λ)max〖e_ij 〗)〗 Выбираем максимальный элемент max〖(0.4 min〖e_ij 〗+0.6 max〖e_ij 〗)〗=max{-14;-6.6;-6} По данному критерию следует выбрать стратегию E_3. Р-критерий произведений Это более нейтральный критерий по сравнению с принципом максимина и критерием азартного игрока. Критерий произведений производит некое «выравнивание» между большими и малыми значениями e_ij. Прибавляем ко всем значением константу c=21. Выбираем максимальный элемент max{66;1620;1386}=1620 По данному критерию следует выбрать стратегию E_2. BL-критерий Байеса-Лапласа Критерий используют в условиях частичной неопределенности и который основан на поиске решения, дающего максимальный средний выигрыш при априорно известных вероятностях состояний природы. Пусть вероятности состояний спроса: 0,2; 0,5; 0,3 Выбираем максимальный элемент max{-15.5;-8.8;-10.5}=-8.8 По данному критерию следует выбрать стратегию E_2. HL-критерий Ходжа-Лемана Найдем оптимальное решение по HL-критерию Ходжа-Лемана, который используют в условиях частичной неопределенности. Он опирается одновременно на критерии BL и ММ путем введения некоторого параметра 0≤ν≤1, выражающего степень доверия к используемому распределению вероятностей. Если это доверие велико, то акцент делается на BL-критерий, иначе — на ЛСИ-крнтерий. Z_HL=max┬i(ν∑▒e_ij q_j+(1-ν) min┬j〖e_ij 〗 ); ν=0.6,q={0,2; 0,5; 0,3} Выбираем максимальный элемент max{-17.3;-10.08;-12.3}=-10.08 По данному критерию следует выбрать стратегию E_2. G-критерий Гермейера Критерий также рекомендуется использовать в условиях частичной неопределенности при оценке потерь ЛИР (элементы матрицы выигрышей e_ij<0). Критерий ориентирован на поиск решений, которые не считаются заведомо худшими, чем другие Z_G=max┬imin┬j〖e_ij q_j 〗 ; q={0,2; 0,5; 0,3} Выбираем максимальный элемент max{-7.5;-5.5;-7.5}=-5.5 По данному критерию следует выбрать стратегию E_2. Анализ решений, полученных по всем критериям, показывает, что критерии не дают единогласного решения: решение E_1 не выгодно с любых точек зрения; решение E_2 рекомендуют MM-, Р-, BL-, HL-, G-критерии; решение E_3 рекомендуют S и HW-критерии. Таким образом, более надежным будет решение E_2 (минимальная проверка). Цель работы Целью работы является приобретение навыков по анализу систем с применением основ теории дифференциальных уравнений и методов решения краевых задач Задание Найти собственные значения и собственные функции краевой задачи. y^»+9y^’=0,y(0)=0,y(l)=0 Решение: Собственные значения λ и функции y являются множеством нетривиальных решений задачи: y^»+9y^’+λy=0 y(0)=0,y(l)=0 Составляем характеристическое уравнение: k^2+9k+λ=0,k_1,2=(-9±√(81-4λ))/2 1) 81-4λ>0, тогда имеем два действительных корня k_1,2 и общее решение: y=C_1 e^(k_1 x)+C_2 e^(k_2 x) Подставляем граничные условия y(0)=0,y(l)=0: {■(C_1+C_2=0@C_1 e^(k_1 l)+C_2 e^(k_2 l)=0)┤ Данная система имеет только нулевое решение, т.е. y≡0. 2) 81-4λ=0,λ=20.25,k_1,2=-4.5 и общее решение: y=(C_1+C_2 x) e^(-4.5x) Подставляем граничные условия y(0)=0,y(l)=0: {■(C_1=0@(C_1+C_2 l) e^(-4.5l)=0)┤⟹{■(C_1=0@C_2 le^(-4.5l)=0)┤⟹{■(C_1=0@C_2=0)┤ Данная система имеет только нулевое решение, т.е. y≡0. 3) 81-4λ<0, тогда получаем два комплексных корня k_1,2=(-9±√(4λ-81) i)/2=-4.5±i√(λ-81/4) Общее решение: y=e^(-4.5x) (C_1 cos(x√(λ-81/4))+C_2 sin(x√(λ-81/4)) ) Подставляем граничные условия y(0)=0,y(l)=0: {■(C_1=0@e^(-4.5l) (C_1 cos(l√(λ-81/4))+C_2 sin(l√(λ-81/4)) )=0)┤ Отсюда C_2 sin(l√(λ-81/4))=0 sin(l√(λ-81/4))=0⟹l√(λ-81/4)=πn,n∈Z λ-81/4=(πn/l)^2,λ_n=20.25+(πn/l)^2 Получили собственные значения и собственные функции краевой задачи: λ_n=20.25+(πn/l)^2 y_n=Ce^(-4.5x) sin(πnx/l),n∈Z
О сайте
Ссылка на первоисточник:
https://www.irgups.ru/abitur/spo/specialty/krizht
Поделитесь в соцсетях:
