Задание по дисциплине "Математика" для ЭИОС МЭБИК (moodle.domebik.ru).

Автор статьи

Валерия

Наши авторы

Эксперт по сдаче вступительных испытаний в ВУЗах

Билет № 11 Вопрос № 1. Дифференцируемая функция, производная, геометрический смысл производной и дифференциала. Ограниченная функция. Теорема Ферма. Вопрос №2. Числовой ряд, сходимость числового ряда. Критерий Коши сходимости числового ряда, необходимое условие сходимости, достаточное условие расходимости. Вопрос №3. Определенный интеграл. Свойства определенного интеграла. Задача. Найти несобственный интеграл

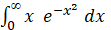Билет № 12 Вопрос №1. Дифференцируемая функция, производная, дифференциал. Геометрический смысл производной и дифференциала. Формула Лагранжа. Вопрос №2. Алгоритм нахождения точных граней функции многих переменных, заданной на замкнутом ограниченном множестве, в том числе линейной функции многих переменных на замкнутом множестве с линейными границами. Вопрос №3. Интеграл с переменным верхним пределом. Теорема о существовании первообразной для непрерывной функции. Формула Ньютона-Лейбница. Задача. . Исследовать числовой ряд на абсолютную и условную сходимость

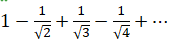Билет № 13 Вопрос № 1. Непрерывная функция. Дифференцируемая функция, производная, дифференциал. Геометрический смысл производной и дифференциала. Теорема Ролля. Вопрос №2. Условный экстремум функции многих переменных. Способы нахождения точек условного экстремума функции многих переменных. Вопрос №3. Определенный интеграл. Свойства определенного интеграла. Задача. Найти несобственный интеграл

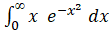Билет № 14 Вопрос №1. Дифференцируемая функция, производная, дифференциал. Теорема Коши. Правило Лопиталя. Вопрос №2. Числовой ряд с неотрицательными членами. Признаки сходимости знакоположительных числовых рядов. Вопрос №3. Первообразная. Неопределенный интеграл, его свойства, способы интегрирования. Задача. Найти определенный интеграл

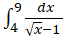Билет № 15 Вопрос № 1. Монотонная функция. Дифференцируемая функция. Достаточное условие возрастания и убывания функции. Вопрос №2. Экстремум функции многих переменных, в том числе двух переменных. Необходимое и достаточное условие существования точки локального экстремума функции многих переменных, в том числе двух переменных. Вопрос №3. Интеграл с переменным верхним пределом. Теорема о существовании первообразной для непрерывной функции. Формула Ньютона-Лейбница. Задача. Исследовать числовой ряд на абсолютную и условную сходимость Билет № 15 Вопрос № 1. Монотонная функция. Дифференцируемая функция. Достаточное условие возрастания и убывания функции. Вопрос №2. Экстремум функции многих переменных, в том числе двух переменных. Необходимое и достаточное условие существования точки локального экстремума функции многих переменных, в том числе двух переменных. Вопрос №3. Интеграл с переменным верхним пределом. Теорема о существовании первообразной для непрерывной функции. Формула Ньютона-Лейбница. Задача. Исследовать числовой ряд на абсолютную и условную сходимость

Похожие ответы, выполненные работы

или напишите нам прямо сейчас

Написать в MAX Написать в Telegram Написать в WhatsApp

О сайте

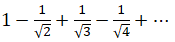
Ссылка на первоисточник:

http://dnmu.ru

Оставить комментарий

Inna Petrova 18 минут назад

Нужно пройти преддипломную практику у нескольких предметов написать введение и отчет по практике так де сдать 4 экзамена после практики

Иван, помощь с обучением 25 минут назад

Inna Petrova, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Коля 2 часа назад

Здравствуйте, сколько будет стоить данная работа и как заказать?

Иван, помощь с обучением 2 часа назад

Николай, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Инкогнито 5 часов назад

Сделать презентацию и защитную речь к дипломной работе по теме: Источники права социального обеспечения. Сам диплом готов, пришлю его Вам по запросу!

Иван, помощь с обучением 6 часов назад

Здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Василий 12 часов назад

Здравствуйте. ищу экзаменационные билеты с ответами для прохождения вступительного теста по теме Общая социальная психология на магистратуру в Московский институт психоанализа.

Иван, помощь с обучением 12 часов назад

Василий, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Анна Михайловна 1 день назад

Нужно закрыть предмет «Микроэкономика» за сколько времени и за какую цену сделаете?

Иван, помощь с обучением 1 день назад

Анна Михайловна, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Сергей 1 день назад

Здравствуйте. Нужен отчёт о прохождении практики, специальность Государственное и муниципальное управление. Планирую пройти практику в школе там, где работаю.

Иван, помощь с обучением 1 день назад

Сергей, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Инна 1 день назад

Добрый день! Учусь на 2 курсе по специальности земельно-имущественные отношения. Нужен отчет по учебной практике. Подскажите, пожалуйста, стоимость и сроки выполнения?

Иван, помощь с обучением 1 день назад

Инна, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Студент 2 дня назад

Здравствуйте, у меня сегодня начинается сессия, нужно будет ответить на вопросы по русскому и математике за определенное время онлайн. Сможете помочь? И сколько это будет стоить? Колледж КЭСИ, первый курс.

Иван, помощь с обучением 2 дня назад

Ольга 2 дня назад

Требуется сделать практические задания по математике 40.02.01 Право и организация социального обеспечения семестр 2

Иван, помощь с обучением 2 дня назад

Ольга, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Вика 3 дня назад

сдача сессии по следующим предметам: Этика деловых отношений - Калашников В.Г. Управление соц. развитием организации- Пересада А. В. Документационное обеспечение управления - Рафикова В.М. Управление производительностью труда- Фаизова Э. Ф. Кадровый аудит- Рафикова В. М. Персональный брендинг - Фаизова Э. Ф. Эргономика труда- Калашников В. Г.

Иван, помощь с обучением 3 дня назад

Вика, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Игорь Валерьевич 3 дня назад

здравствуйте. помогите пройти итоговый тест по теме Обновление содержания образования: изменения организации и осуществления образовательной деятельности в соответствии с ФГОС НОО

Иван, помощь с обучением 3 дня назад

Игорь Валерьевич, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Вадим 4 дня назад

Пройти 7 тестов в личном кабинете. Сооружения и эксплуатация газонефтипровод и хранилищ

Иван, помощь с обучением 4 дня назад

Вадим, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Кирилл 4 дня назад

Здравствуйте! Нашел у вас на сайте задачу, какая мне необходима, можно узнать стоимость?

Иван, помощь с обучением 4 дня назад

Кирилл, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Oleg 4 дня назад

Требуется пройти задания первый семестр Специальность: 10.02.01 Организация и технология защиты информации. Химия сдана, история тоже. Сколько это будет стоить в комплексе и попредметно и сколько на это понадобится времени?

Иван, помощь с обучением 4 дня назад

Oleg, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Валерия 5 дней назад

ЗДРАВСТВУЙТЕ. СКАЖИТЕ МОЖЕТЕ ЛИ ВЫ ПОМОЧЬ С ВЫПОЛНЕНИЕМ практики и ВКР по банку ВТБ. ответьте пожалуйста если можно побыстрее , а то просто уже вся на нервяке из-за этой учебы. и сколько это будет стоить?

Иван, помощь с обучением 5 дней назад

Валерия, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Инкогнито 5 дней назад

Здравствуйте. Нужны ответы на вопросы для экзамена. Направление - Пожарная безопасность.

Иван, помощь с обучением 5 дней назад

Иван неделю назад

Защита дипломной дистанционно, "Синергия", Направленность (профиль) Информационные системы и технологии, Бакалавр, тема: «Автоматизация приема и анализа заявок технической поддержки

Иван, помощь с обучением неделю назад

Иван, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Дарья неделю назад

Необходимо написать дипломную работу на тему: «Разработка проекта внедрения CRM-системы. + презентацию (слайды) для предзащиты ВКР. Презентация должна быть в формате PDF или формате файлов PowerPoint! Институт ТГУ Росдистант. Предыдущий исполнитель написал ВКР, но работа не прошла по антиплагиату. Предыдущий исполнитель пропал и не отвечает. Есть его работа, которую нужно исправить, либо переписать с нуля.

Иван, помощь с обучением неделю назад

Дарья, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru