Автор статьи
Валерия
Эксперт по сдаче вступительных испытаний в ВУЗах
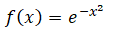Билет № 2
Вопрос №1. Функция. Предел функции. Правила нахождения предела.
Вопрос №2. Интегрируемая функция, определенный интеграл. Классы интегрируемых функций.
Вопрос №3. Экстремум функции многих переменных, в том числе двух переменных. Необходимое и достаточное условие существования точки локального экстремума функции многих переменных, в том числе двух переменных.
Задача. Найти асимптоты функции 
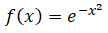Билет № 3
Вопрос № 1. Функция. Предел функции. Теоремы о локальном поведении функции.
Вопрос №2. Первообразная. Вопрос единственности первообразной. Неопределенный интеграл.
Вопрос №3. Числовой ряд с неотрицательными членами. Признаки сходимости знакоположительных числовых рядов.
Задача. Найти точки локального экстремума функции двух переменных 
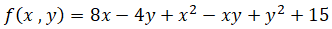Билет № 4
Вопрос №1. Непрерывная функция. Классификация точек разрыва. Локальные свойства непрерывных функций.
Вопрос №2. Первообразная. Неопределенный интеграл, его свойства, способы интегрирования.
Вопрос №3. Экстремум функции многих переменных, в том числе двух переменных. Необходимое и достаточное условие существования точки локального экстремума функции многих переменных, в том числе двух переменных.
Задача. Исследовать числовой ряд на абсолютную и условную сходимость 
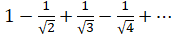Билет № 5
Вопрос № 1. Непрерывная функция. Ограниченная функция. Теоремы Вейерштрасса.
Вопрос №2. Интегрируемая функция, определенный интеграл. Необходимое и достаточное условие интегрируемости ограниченной функции.
Вопрос №3. Числовой ряд, сходимость числового ряда. Критерий Коши сходимости числового ряда, необходимое условие сходимости, достаточное условие расходимости.
Задача. Найти точки локального экстремума функции двух переменных
О сайте
Ссылка на первоисточник:
http://daok-derbent.ru/
Поделитесь в соцсетях: